未来的研究方向里有好多要用到逆向工程的地方
感觉是绕不开逆向了,因此打算猛猛突击一下
IDA使用基础
常用快捷键
| 快捷键 |
功能 |
| F2 |
添加断点 |
| F4 |
开始运行 |
| F5 |
反编译成伪代码 |
| F7 |
进入函数 |
| F8 |
单步调试 |
| F9 |
运行到下一个断点 |
| Space |
切换反汇编窗口(列表视图&图形视图) |
| Tab |
返回栈视图 |
| ESC |
跳转到返回前的地址 |
| / |
添加注释 |
| N |
修改变量名 |
| D |
代码解析成数据 |
| C |
数据解析成代码 |
| G |
跳转到指定地址查看 |
| H |
转换为十进制数 |
| Q |
转换为十六进制数 |
| R |
转换为字符 |
| X |
查看函数的交叉引用 |
| Y |
指定当前函数的命名 |
| Shift+F12 |
打开字符串窗口 |
| Shift+E |
批量复制数据为字符串或者c数组格式 |
正常显示中文字符串
Options → Strings → Default 8-bit
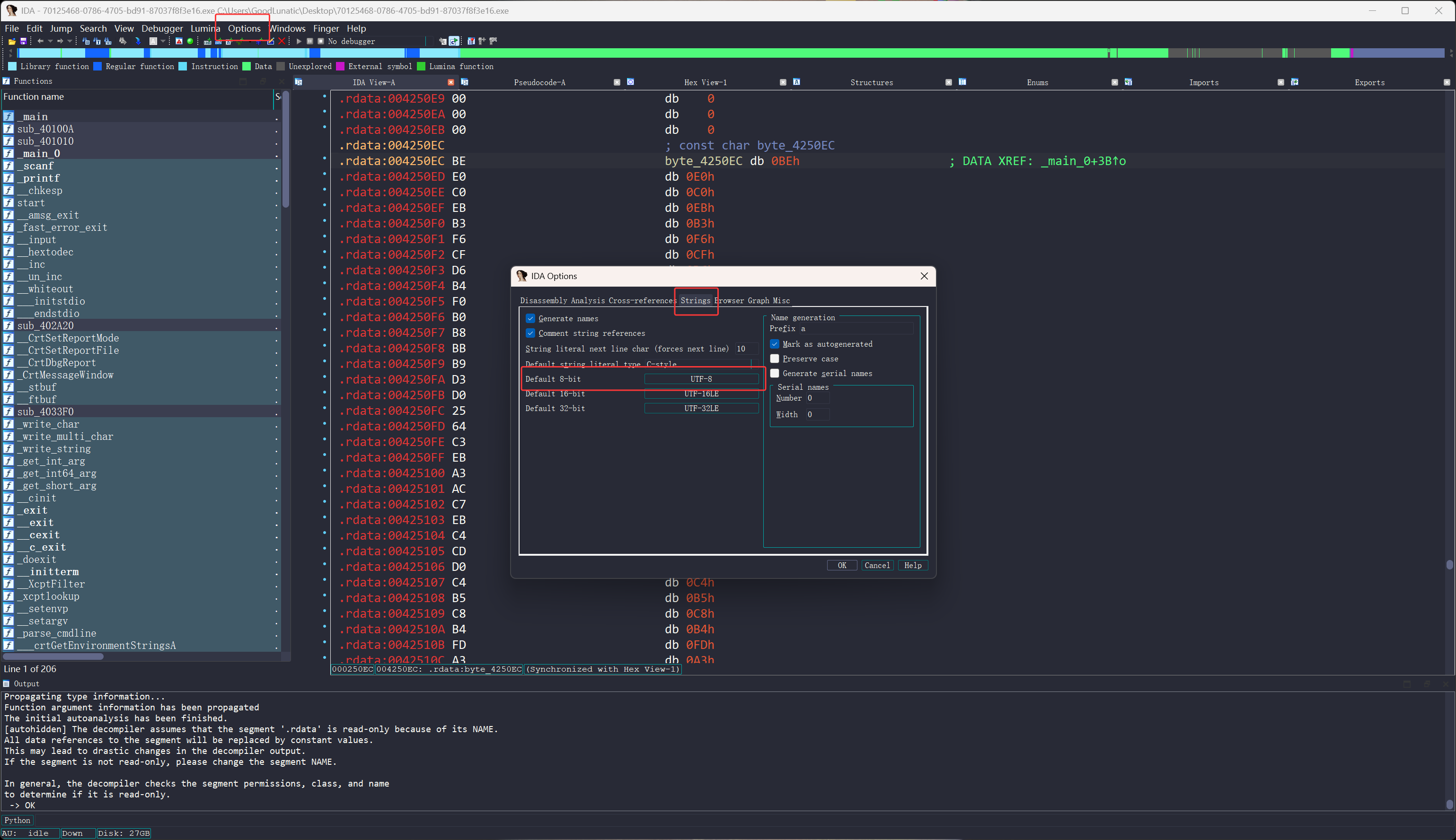
点击UTF-8然后右键新插入一个gbk,然后选中并保存
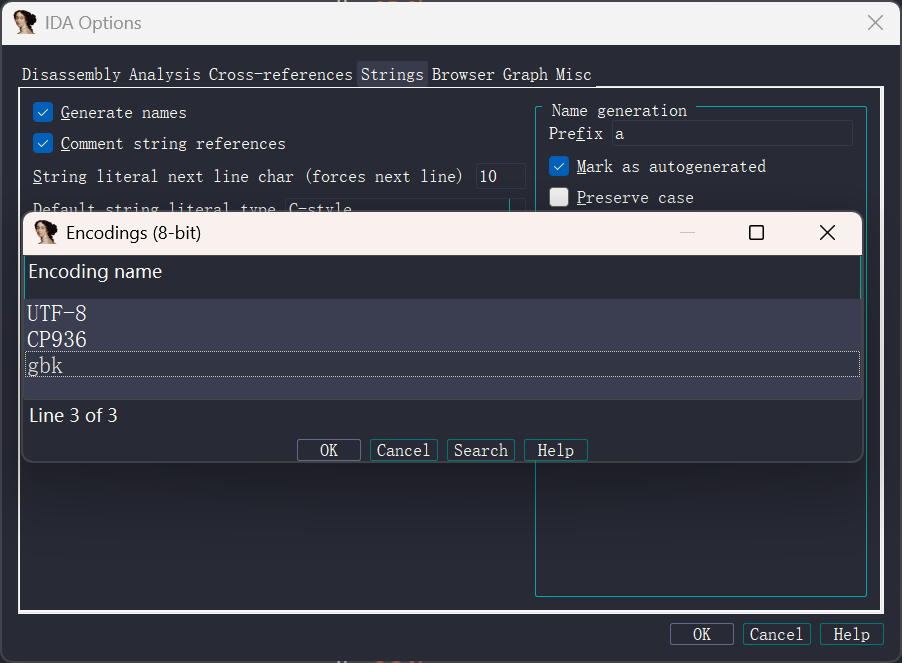
最后点击字符串,然后按键盘上的ALT+A,选中C-style即可
如果修改后中文没有正常显示,可以尝试点击反编译后的变量按F5重新反编译
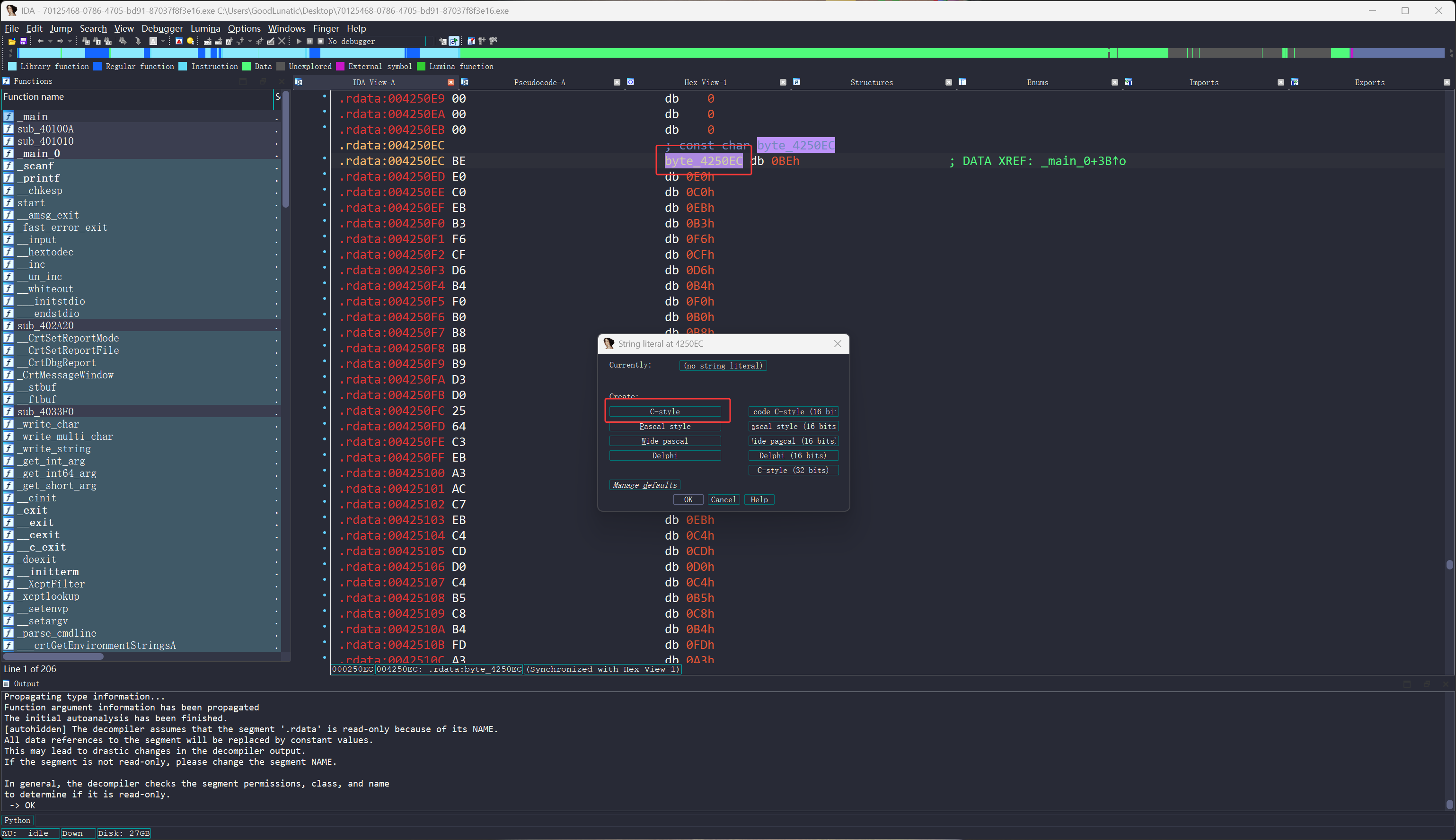
例题-BUU-内涵的软件
逆向中常见的数据类型
| 数据类型 |
位数 |
| 1 byte = 8 bit |
8 位 |
| 1 word = 2 byte |
16 位 |
| 1 dword(Double Word) = 2 word = 4 byte |
32 位 |
| 1 qword(Quadra Word) = 2 dword = 8 byte |
64 位 |
|
|
| uint32_t |
32 位 |
| uint64_t |
64 位 |
| char (-127-128) |
8 位 |
| unsigned char (0-255) |
8 位 |
|
|
| float |
32位 |
| double |
64 位 |
汇编基础
| 汇编指令 |
示例 |
含义 |
说明 |
| MOV |
MOV EAX, ECX |
EAX = ECX |
将ECX的值赋给EAX |
| ADD |
ADD EAX, ECX |
EAX += ECX |
将EAX的值加上ECX的值 |
| SUB |
SUB EAX, ECX |
EAX -= ECX |
将EAX的值减去ECX的值 |
| INC |
INC EAX |
EAX++ |
将EAX的值+1 |
| DEC |
DEX EAX |
EAX– |
将EAX的值-1 |
| LEA |
LEA EAX, ECX |
EAX = ECX的地址 |
将ECX的地址存入EAX |
| AND |
AND EAX, ECX |
EAX = EAX & ECX |
EAX与ECX进行与运算 |
| OR |
OR EAX, ECX |
EAX = EAX | ECX |
EAX与ECX进行或运算 |
| XOR |
XOR EAX, ECX |
EAX = EAX ^ ECX |
EAX与ECX进行异或运算 |
| NOT |
NOT EAX |
EAX = ~EAX |
将EAX的值取反 |
| SHL |
SHL EAX, 3 |
EAX = EAX « 3 |
将EAX的值左移三位 |
| SHR |
SHR EAX, 3 |
EAX = EAX » 3 |
将EAX的值右移三位 |
| CMP |
CMP EAX, ECX |
if(EAX == ECX) ZF = 1
else ZF = 0 |
对EAX和ECX的值进行比较并根据比较结果设置ZF标志的值 |
| TEST |
TEST EAX, EAX |
if(EAX == 0) ZF = 1
else ZF = 0 |
将EAX的值与0进行比较并根据比较结果设置ZF标志的值 |
| JE[JZ] |
JZ 04001000 |
if(ZF == 1)
GOTO 04001000 |
若ZF为1则跳转至 04001000 |
| JNE[JNZ] |
JNZ 04001000 |
if(ZF == 0)
GOTO 04001000 |
若ZF为0则跳转至 04001000 |
| JMP |
JMP 04001000 |
GOTO 04001000 |
直接跳转至 04001000 |
| CALL |
CALL printf
CALL $+5 |
|
调用函数printf
跳转到下一条指令 |
| PUSH |
PUSH EAX |
|
将EAX的值压入栈顶 |
| POP |
POP EAX |
|
将栈顶的值弹给EAX |
一些常用的寄存器:
| 32位 (x86) |
64位 (x64) |
用途 |
| EAX |
RAX |
累加器(Accumulator),算术运算、函数返回值 |
| EBX |
RBX |
基址寄存器(Base),常用于存储指针 |
| ECX |
RCX |
计数器(Counter),LOOP指令、字符串操作 |
| EDX |
RDX |
数据寄存器(Data),辅助EAX(如MUL/DIV) |
| ESI |
RSI |
源索引(Source Index),字符串/内存操作 |
| EDI |
RDI |
目标索引(Destination Index),字符串/内存操作 |
| ESP |
RSP |
栈指针(Stack Pointer),指向当前栈顶 |
| EBP |
RBP |
基址指针(Base Pointer),函数栈帧 |
|
|
|
| EIP |
RIP |
存储下一条要执行的指令地址 |
| EFLAGS |
RFLAGS |
存储 CPU 状态标志(如 ZF, CF, SF 等) |
常见的编码与加密
base64
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
char base64_table[] = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"
int __fastcall base64_encode(char *Str2, char *Str)
{
int v3; // [rsp+24h] [rbp-1Ch]
int v4; // [rsp+34h] [rbp-Ch]
int v5; // [rsp+38h] [rbp-8h]
int v6; // [rsp+3Ch] [rbp-4h]
v3 = strlen(Str);
if ( v3 % 3 )
v6 = 4 * (v3 / 3 + 1);
else
v6 = 4 * (v3 / 3);
Str2[v6] = 0;
v5 = 0;
v4 = 0;
while ( v6 - 2 > v5 )
{
Str2[v5] = base64_table[(unsigned __int8)Str[v4] >> 2]; // 右移2位,获得第一个字符前6位的数据
Str2[v5 + 1] = base64_table[(16 * (Str[v4] & 3)) | ((unsigned __int8)Str[v4 + 1] >> 4)]; // 获取第二个6位
Str2[v5 + 2] = base64_table[(4 * (Str[v4 + 1] & 0xF)) | ((unsigned __int8)Str[v4 + 2] >> 6)]; // 获得第三个6位
Str2[v5 + 3] = base64_table[Str[v4 + 2] & 0x3F]; // 获得第四个6位
v4 += 3;
v5 += 4;
}
if ( v3 % 3 == 1 )
{
Str2[v5 - 2] = "=";
Str2[v5 - 1] = "=";
}
else if ( v3 % 3 == 2 )
{
Str2[v5 - 1] = "=";
}
return putchar("\n");
}
|
RC4加密算法
TEA系列加密算法
TEA
加密和解密的示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
void encrypt(unsigned int* v, unsigned int* key) {
unsigned int l = v[0], r = v[1], sum = 0, delta = 0x9e3779b9;
for (int i = 0; i < 32; i++) {
sum += delta;
l += ((r << 4) + key[0]) ^ (r + sum) ^ ((r >> 5) + key[1]);
r += ((l << 4) + key[2]) ^ (l + sum) ^ ((l >> 5) + key[3]);
}
v[0] = l;
v[1] = r;
}
void decrypt(unsigned int* v, unsigned int* key) {
unsigned int l = v[0], r = v[1], sum = 0, delta = 0x9e3779b9;
sum = delta *32;
for (int i = 0; i < 32; i++) {
r -= ((l << 4) + key[2]) ^ (l + sum) ^ ((l >> 5) + key[3]);
l -= ((r << 4) + key[0]) ^ (r + sum) ^ ((r >> 5) + key[1]);
sum -= delta;
}
v[0] = l;
v[1] = r;
}
|
解密脚本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
#include<stdio.h>
int main(){
int n;//pw的个数
unsigned int pw[]={};//可改
unsigned int v0;
unsigned int v1;
unsigned int sum;
unsigned int key[4]={1,2,3,4};//可改
for(int i=0;i<n/2;i++)
{
v0=pw[2*i];
v1=pw[2*i+1];
sum=-32*0x61C88647;
for(int i=0;i<32;i++)
{
v1 -= ((v0 >> 5) + key[3] )^ (16 * v0 + key[2]) ^ (sum + v0);//容易魔改
v0 -= ((v1 >> 5) + key[1]) ^ (16 * v1 + key[0]) ^ (sum + v1);
sum += 0x61C88647;//容易魔改
}
for (int j = 0; j<=3; j++)
{
printf("%c", (v0 >> (j * 8)) & 0xFF);
}
for (int j = 0; j<=3; j++)
{
printf("%c", (v1 >> (j * 8)) & 0xFF);
}
}
}
|
比赛中用到的一些代码
处理原始字节数据版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
|
#include <iostream>
#include <cstdint>
void tea_decrypt(uint32_t* v, uint32_t* key) {
uint32_t l = v[0];
uint32_t r = v[1];
uint32_t sum = 32 * 0x414554; // 加密的总delta和
for (int i = 0; i < 32; ++i) {
r -= ((l << 4) + key[2]) ^ (l + sum) ^ ((l >> 5) + key[3]);
l -= ((r << 4) + key[0]) ^ (r + sum) ^ ((r >> 5) + key[1]);
sum -= 0x414554;
}
v[0] = l;
v[1] = r;
}
int main() {
// 加密后的数据(小端序)
uint8_t encrypted[] = {
0xE4, 0x6E, 0x00, 0xF0,
0x91, 0x73, 0x9A, 0xBE,
0xCA, 0xF1, 0x2A, 0x60,
0x0E, 0x8F, 0x74, 0x83,
0xE0, 0x8E, 0x6C, 0x34,
0xD7, 0x99, 0xDE, 0x36,
0x8B, 0x86, 0xC4, 0x90,
0xC2, 0x0B, 0xC4, 0x59
};
// 密钥(小端序)
uint8_t key_bytes[] = {
0xEF, 0xBE, 0xAD, 0xDE,
0x0D, 0xF0, 0xAD, 0xBA,
0xDE, 0xC0, 0xAD, 0xDE,
0xCC, 0x10, 0xAD, 0xDE
};
// 将字节数组转换为4个32位整数(注意小端序)
uint32_t key[4];
for (int i = 0; i < 4; i++) {
key[i] = (key_bytes[4*i+3] << 24) | (key_bytes[4*i+2] << 16) |
(key_bytes[4*i+1] << 8) | key_bytes[4*i];
}
// 0xDEADBEEF 0xBAADF00D 0xDEADC0DE 0xDEAD10CC
int num_blocks = sizeof(encrypted) / 8; // 8个32位整数
for (int i = 0; i < num_blocks; i++) {
// 将加密数据转换为32位整数(小端序)
uint32_t v[2];
v[0] = (encrypted[8*i+3] << 24) | (encrypted[8*i+2] << 16) |
(encrypted[8*i+1] << 8) | encrypted[8*i];
v[1] = (encrypted[8*i+7] << 24) | (encrypted[8*i+6] << 16) |
(encrypted[8*i+5] << 8) | encrypted[8*i+4];
// 一次解密两个32位整数
tea_decrypt(v, key);
// 输出解密结果(转换为字节)
for (int j = 0; j < 4; j++) {
printf("%c", (v[0] >> (j * 8)) & 0xFF);
}
for (int j = 0; j < 4; j++) {
printf("%c", (v[1] >> (j * 8)) & 0xFF);
}
}
return 0;
}
|
XTEA
加密和解密的示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
void xtea_encrypt(uint32_t* v, uint32_t* key) {
uint32_t v0 = v[0];
uint32_t v1 = v[1];
uint32_t sum = 0;
uint32_t delta = 0x9E3779B9; //0x9E3779B9=-0x61C88647
for (int i = 0; i < 32; i++) {
v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
sum += delta; // 如果 delta=0x61C88647, 这里就是 sum -= delta
v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum >> 11) & 3]);
}
v[0] = v0;
v[1] = v1;
}
void xtea_decrypt(uint32_t* v, uint32_t* key) {
uint32_t v0 = v[0];
uint32_t v1 = v[1];
uint32_t sum = 32 * 0x9E3779B9; // 加密的总和
uint32_t delta = 0x9E3779B9;
for (int i = 0; i < 32; i++) {
v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum >> 11) & 3]);
sum -= delta;
v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
}
v[0] = v0;
v[1] = v1;
}
|
比赛中用到的一些脚本
处理原始字节数据版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
|
#include <iostream>
#include <cstdint>
void xtea_decrypt(uint32_t* v, uint32_t* key) {
uint32_t l = v[0];
uint32_t r = v[1];
uint32_t sum = 32 * 0x9E3779B9; // XTEA的总delta和(32轮)
uint32_t delta = 0x9E3779B9;
for (int i = 0; i < 32; ++i) {
r -= (((l << 4) ^ (l >> 5)) + l) ^ (key[(sum >> 11) & 3] + sum);
sum -= delta;
l -= (((r << 4) ^ (r >> 5)) + r) ^ (key[sum & 3] + sum);
}
v[0] = l;
v[1] = r;
}
int main() {
// 加密后的数据(小端序)
uint8_t encrypted[] = {
0xD1, 0x36, 0x0D, 0x59,
0xE2, 0xB5, 0xA9, 0x6F,
0xAD, 0x90, 0x71, 0xDA,
0xA0, 0x0A, 0x4B, 0xC5,
0x54, 0xED, 0xA5, 0xAD,
0x84, 0x7F, 0xD0, 0x4A,
0xC0, 0xF3, 0x4C, 0x8A,
0x2F, 0xB2, 0xEF, 0x7F
};
// 密钥(小端序)
uint8_t key_bytes[] = {
0x0D, 0x00, 0x00, 0x00,
0x00, 0x00, 0x00, 0x00,
0x07, 0x00, 0x00, 0x00,
0x21, 0x00, 0x00, 0x00
};
// 将字节数组转换为4个32位整数(小端序)
uint32_t key[4];
for (int i = 0; i < 4; i++) {
key[i] = (key_bytes[4*i+3] << 24) | (key_bytes[4*i+2] << 16) |
(key_bytes[4*i+1] << 8) | key_bytes[4*i];
}
int num_blocks = sizeof(encrypted) / 8; // 每个块8字节
for (int i = 0; i < num_blocks; i++) {
// 将加密数据转换为32位整数(小端序)
uint32_t v[2]; // 数组元素每个为4字节
v[0] = (encrypted[8*i+3] << 24) | (encrypted[8*i+2] << 16) |
(encrypted[8*i+1] << 8) | encrypted[8*i];
v[1] = (encrypted[8*i+7] << 24) | (encrypted[8*i+6] << 16) |
(encrypted[8*i+5] << 8) | encrypted[8*i+4];
// XTEA解密
xtea_decrypt(v, key);
// 输出解密结果(转换为字节,小端序)
for (int j = 0; j < 4; j++) {
printf("%c", (v[0] >> (j * 8)) & 0xFF);
}
for (int j = 0; j < 4; j++) {
printf("%c", (v[1] >> (j * 8)) & 0xFF);
}
}
return 0;
}
|
处理32位整数版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
#include <iostream>
void xtea_decrypt(uint32_t *v, uint32_t *key)
{
uint32_t l = v[0];
uint32_t r = v[1];
uint32_t sum = 32 * 0x9E3779B9; // XTEA的总delta和(32轮)
uint32_t delta = 0x9E3779B9;
for (int i = 0; i < 32; ++i)
{
r -= (((l << 4) ^ (l >> 5)) + l) ^ (key[(sum >> 11) & 3] + sum);
sum -= delta;
l -= (((r << 4) ^ (r >> 5)) + r) ^ (key[sum & 3] + sum);
}
v[0] = l;
v[1] = r;
}
int main()
{
uint32_t enc[8] =
{// 4x8=32字节
0x590D36D1, 0x6FA9B5E2, 0xDA7190AD, 0xC54B0AA0,
0xADA5ED54, 0x4AD07F84, 0x8A4CF3C0, 0x7FEFB22F
};
uint32_t key[4] = {0x0000000D, 0x00000000, 0x00000007, 0x00000021};
int num_blocks = sizeof(enc) / 8; // 每个块8字节, 所以这里的结果是4
for (int i = 0; i < num_blocks; i++)
{
uint32_t v[2];
v[0] = enc[2 * i];
v[1] = enc[2 * i + 1];
xtea_decrypt(v, key);
// 输出解密结果(转换为字节,小端序)
for (int j = 0; j < 4; j++)
{
printf("%c", (v[0] >> (j * 8)) & 0xFF);
}
for (int j = 0; j < 4; j++)
{
printf("%c", (v[1] >> (j * 8)) & 0xFF);
}
}
return 0;
}
|
XXTEA
加密和解密的示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
void xxtea_encrypt(uint32_t* v, int n, uint32_t key[4]) {
uint32_t y, z, sum;
uint32_t delta = 0x9E3779B9;
uint32_t p, rounds, e;
rounds = 6 + 52 / n;
sum = 0;
z = v[n - 1];
do {
sum += delta;
e = (sum >> 2) & 3;
for (p = 0; p < n - 1; p++) {
y = v[p + 1];
v[p] += ((z >> 5 ^ y << 2) + (z << 3 ^ y >> 4)) ^ ((sum ^ y) + (key[(p & 3) ^ e] ^ z));
z = v[p];
}
y = v[0];
v[n - 1] += ((z >> 5 ^ y << 2) + (z << 3 ^ y >> 4)) ^ ((sum ^ y) + (key[(p & 3) ^ e] ^ z));
z = v[n - 1];
} while (--rounds);
}
void xxtea_decrypt(uint32_t* v, int n, uint32_t key[4]) {
uint32_t y, z, sum;
uint32_t delta = 0x9E3779B9;
uint32_t p, rounds, e;
rounds = 6 + 52 / n;
sum = rounds * delta;
y = v[0];
do {
e = (sum >> 2) & 3;
for (p = n - 1; p > 0; p--) {
z = v[p - 1];
v[p] -= ((z >> 5 ^ y << 2) + (z << 3 ^ y >> 4)) ^ ((sum ^ y) + (key[(p & 3) ^ e] ^ z));
y = v[p];
}
z = v[n - 1];
v[0] -= ((z >> 5 ^ y << 2) + (z << 3 ^ y >> 4)) ^ ((sum ^ y) + (key[(p & 3) ^ e] ^ z));
y = v[0];
sum -= delta;
} while (--rounds);
}
|
解密脚本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
#include <stdio.h>
#include <stdlib.h>
#define delta 0x9e3779b9
int main()
{
unsigned int v[8] = {0x10BD3B47, 0x6155E0F9, 0x6AF7EBC5, 0x8D23435F, 0x1A091605, 0xD43D40EF, 0xB4B16A67, 0x6B3578A9};//可改
unsigned int key[4] = {0x00001234, 0x00002345, 0x00004567, 0x00006789};//可改
unsigned int sum = 0;
unsigned int y,z,p,rounds,e;
int n = 8;//v的个数
int i = 0;
rounds = 6 + 52/n;//容易魔改
y = v[0];
sum = rounds*delta;
do
{
e = sum >> 2 & 3;
for(p=n-1;p>0;p--)
{
z = v[p-1];
v[p] -= ((((z>>5)^(y<<2))+((y>>3)^(z<<4))) ^ ((key[(p&3)^e]^z)+(y ^ sum)));//容易魔改
y = v[p];
}
z = v[n-1];
v[0] -= (((key[(p^e)&3]^z)+(y ^ sum)) ^ (((y<<2)^(z>>5))+((z<<4)^(y>>3))));//容易魔改
y = v[0];
sum = sum-delta;
}while(--rounds);
for(i=0;i<n;i++)
{
printf("%c%c%c%c",*((char*)&v[i]+0),*((char*)&v[i]+1),*((char*)&v[i]+2),*((char*)&v[i]+3));
//printf("%c%c%c%c",*((char*)&v[i]+3),*((char*)&v[i]+2),*((char*)&v[i]+1),*((char*)&v[i]+0));
}
return 0;
}
|
MD5
SMC
SMC,即Self Modifying Code,动态代码加密技术,指通过修改代码或数据,阻止别人直接静态分析,然后在动态运行程序时对代码进行解密,达到程序正常运行的效果。
SMC一般有俩种破解方法,第一种是找到对代码或数据加密的函数后通过idapython写解密脚本。第二种是动态调试到SMC解密结束的地方dump出来。
常见的混淆
花指令
永恒跳转
构造代码如下
1
2
3
4
5
|
__asm {
_emit 0xE8
_emit 0xFF
//_emit 立即数:代表在这个位置插入一个数据,这里插入的是0xe8
}
|
插入这些代码后,IDA反汇编就会得到如下内容
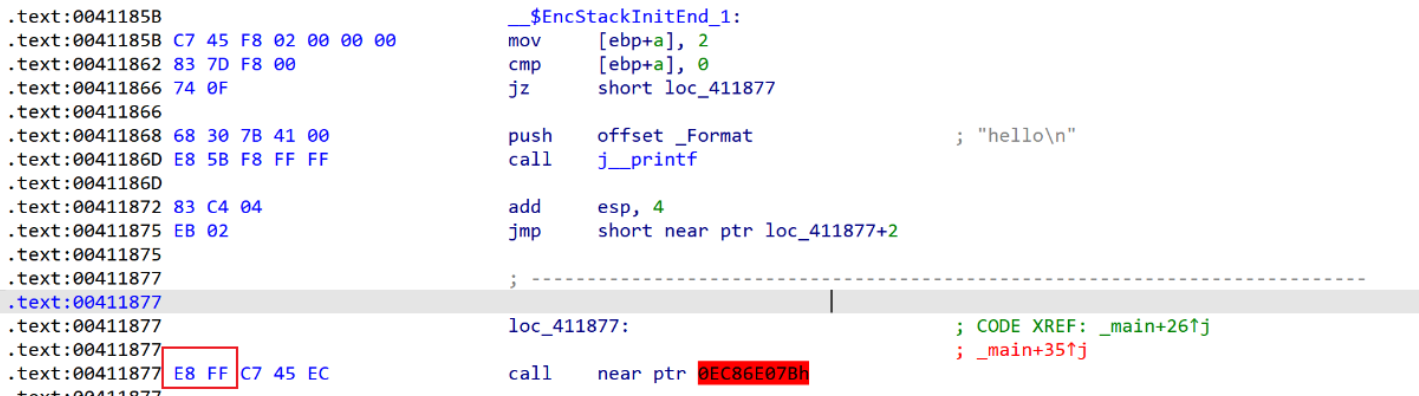
对于这种,我们只要将0xE8该成0x90(NOP指令)即可
jnz和jz互补跳转
构造代码如下
1
2
3
4
5
|
__asm {
jz Label;
jnz Label;
_emit 0xC7;
Label:
|
插入这些代码后,IDA反汇编就会得到如下内容
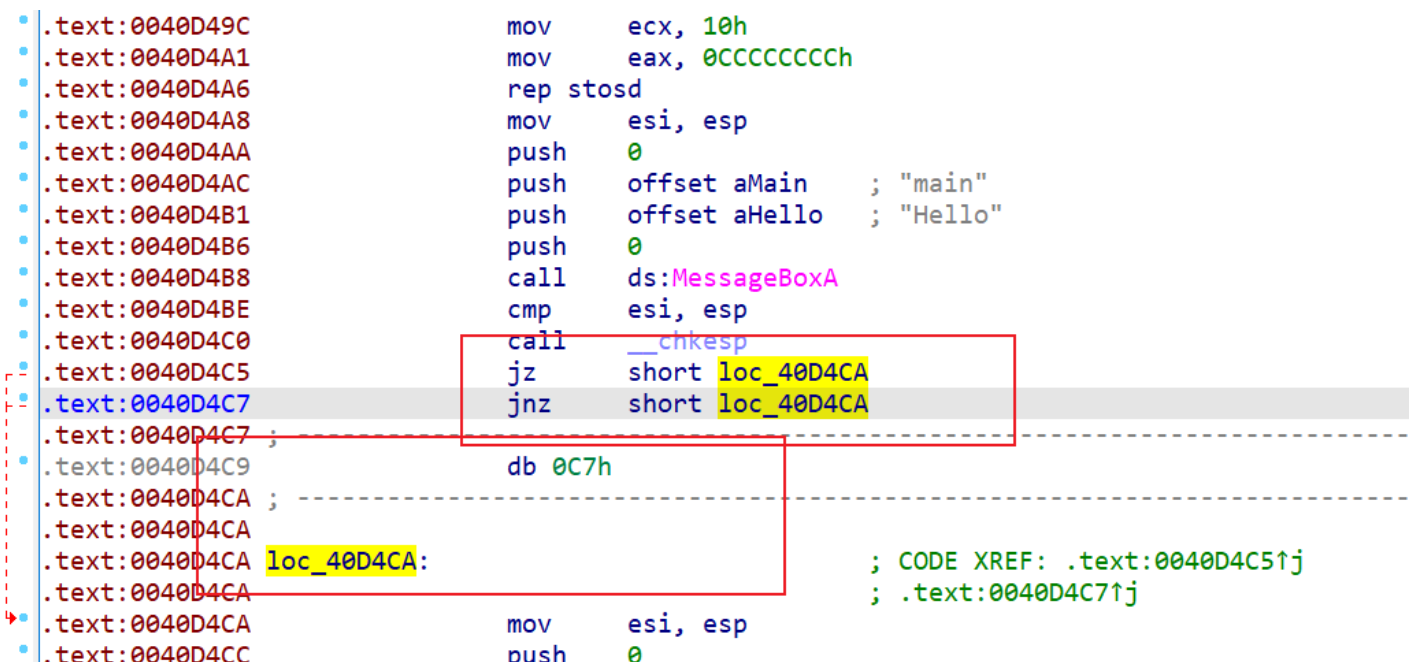
去除花指令的方法:
在准备去除花指令之前,我们需要先调整操作码显示的字节数
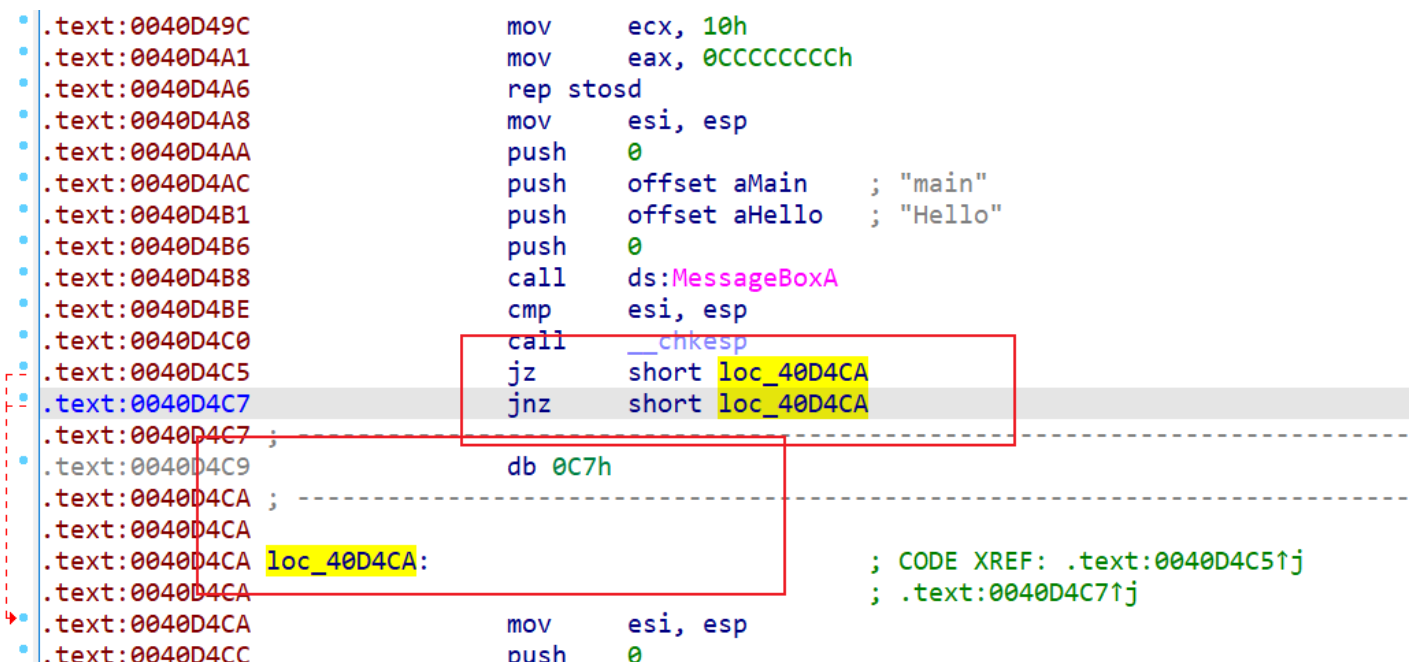
1、点到跳转的那一行,按键盘上的u键,将其解析为数据,然后在E8上右键选择NOP,再按键盘上的c键重新解析为代码,最后在函数名(main)上按一下p键然后F5重新反汇编即可
2、点到跳转的那一行,按键盘上的u键,将其解析为数据,然后点击菜单栏 Edit → Patch Program → Change byte,将0xE8改成0x90,再按键盘上的c键重新解析为代码,最后在函数名(main)上按一下p键然后F5重新反汇编即可
例题1-[HNCTF 2022 WEEK2]e@sy_flower
例题2-[NSSRound#3 Team]jump_by_jump_revenge
例题3-[MoeCTF 2022]chicken_soup
控制流平坦化
OLLVM
常见的壳
可以先把待逆向的文件拖入 DIE(Detect-It-Easy) 中查看是用的什么壳
upx
一种压缩壳,可以尝试直接用upx脱壳
1
2
3
4
|
# 下载
upx: https://github.com/upx/upx
# 使用方法
upx -d re.exe
|
也可以尝试手动脱upx
Python逆向
有部分exe是由 pyinstaller 打包的,通常可以直接根据文件的图标看出来
针对这种exe的逆向,我可以按照如下步骤:
1、使用 pyinstxtractor 先进行解包
pyinstxtractor: https://github.com/extremecoders-re/pyinstxtractor
1
2
3
4
|
# 可以用如下命令进行解包
[+] Usage: pyinstxtractor.py <filename>
python ~/CTF/Reverse/pyinstxtractor/pyinstxtractor.py pyc.exe
# 这里要注意,如果本地版本和出题人打包用的版本不同,某些依赖可能无法正常解包
|
2、反编译解包后得到的 pyc 文件
第一种方法是用如下的在线网站反编译:
1
2
3
|
https://tool.lu/pyc/
https://www.lddgo.net/string/pyc-compile-decompile
https://www.toolkk.com/tools/pyc-decomplie
|
第二中方法就是用本地工具进行反编译,这里有以下三个常用的反编译工具:
uncompyle6: https://github.com/rocky/python-uncompyle6
1
2
3
4
5
6
|
# 直接 pip 安装即可
pip3 install uncompyle6
# 然后将 Script 目录添加到环境变量中
C:\Users\XXX\AppData\Local\Programs\Python\Python38\Scripts
# 之后就可以直接在终端中使用了
uncompyle6 filename.pyc > decompile.py
|
pyinstxtractor: https://github.com/extremecoders-re/pyinstxtractor
1
|
python pyinstxtractor.py reverse_1_PyHaHa.pyc
|
pycdc: https://github.com/zrax/pycdc
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
# 下载并编译
git clone https://github.com/zrax/pycdc.git
mkdir build && cd build
cmake ..
make -j$(nproc)
# 使用方法
Usage: ./pycdc [options] input.pyc
~/CTF/Reverse/pycdc/build/pycdc main.pyc
Options:
-o <filename> Write output to <filename> (default: stdout)
-c Specify loading a compiled code object. Requires the version to be set
-v <x.y> Specify a Python version for loading a compiled code object
--help Show this help text and then exit
|
Tips: 有时候会遇到pyc文件魔术头被修改的情况,可以复制解包后的struct.pyc到要反编译的pyc文件中(就是文件前16个字节)
Unity游戏逆向
参考文章:https://forum.butian.net/share/1294
Unity 游戏的主逻辑一般都保存在 dll 文件中,因此我们需要下个 dnspy 来反编译
然后我们需要打开并反编译 data/Managed/Assembly-CSarp.dll 这个文件
我们可以在 dnspy 的编辑器中右键编辑类或者方法,编辑完后编译
然后左上角-文件-全部保存即可保存我们的修改
一般就是修改分数或者判断逻辑等参数,从而获得 flag
常用的一些逆向工具
Z3 约束求解器
Z3-solver是微软开发的自动定理证明器和约束求解器,能够将复杂问题转化为数学约束条件,然后自动寻找满足所有条件的解。它特别擅长处理包含布尔逻辑、算术运算、位运算等多种约束的复杂问题,广泛应用于程序验证、网络安全、人工智能等领域。Z3通过先进的符号推理和约束求解技术,能够解决传统方法难以处理的非线性约束和复杂逻辑关系,是一个强大的数学问题求解工具。
安装方法: pip3 install z3-solver
基本用法如下,更多用法可以参考官方文档
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
from z3 import *
# 1. 创建变量
x = Int('x') # 整型变量
y = Int('y') # 整型变量
p = Bool('p') # 布尔变量p
q = Bool('q') # 布尔变量q
r = Bool('r') # 布尔变量r
# 2. 创建求解器
s = Solver()
# 3. 添加约束条件
# 数值约束
s.add(x > 0) # x必须大于0
s.add(y > 0) # y必须大于0
s.add(x + y == 10) # x+y等于10
s.add(Implies(p, x > y)) # 如果p为真,则x>y
# 逻辑约束
s.add(Implies(p, q)) # p → q (如果p为真,则q为真)
s.add(r == Not(q)) # r = ¬q (r等于q的否定)
s.add(Or(Not(p), r)) # ¬p ∨ r (p的否定或r为真)
# 4. 检查约束是否可满足
if s.check() == sat:
# 5. 获取解
m = s.model()
print(f"找到解:x = {m[x]}, y = {m[y]}")
print(f"逻辑变量:p = {m[p]}, q = {m[q]}, r = {m[r]}")
else:
print("约束不可满足")
|
示例代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
from z3 import *
enc = [0x0000B1B0, 0x00005678, 0x00007FF2, 0x0000A332, 0x0000A0E8, 0x0000364C, 0x00002BD4, 0x0000C8FE, 0x00004A7C, 0x00000018, 0x00002BE4, 0x00004144, 0x00003BA6, 0x0000BE8C, 0x00008F7E, 0x000035F8, 0x000061AA, 0x00002B4A, 0x00006828, 0x0000B39E, 0x0000B542, 0x000033EC, 0x0000C7D8, 0x0000448C, 0x00009310, 0x00008808, 0x0000ADD4, 0x00003CC2, 0x00000796, 0x0000C940, 0x00004E32, 0x00004E2E, 0x0000924A, 0x00005B5C]
s = Solver()
input = [BitVec(f"input{i}", 8) for i in range(34)] # input0-input33 都是 0-255
var = [BitVec(f"var{i}",32) for i in range(34)] # var0-var31 都是 0-4294967295
# 模拟加密算法
for i in range(34):
var[i] = 47806 * (ZeroExt(24, input[i]) + i) # 高位补零,将8位扩展至32位
if i:
var[i] ^= var[i-1] ^ 0x114514
var[i] %= 51966
# 添加约束条件
for i in range(34):
s.add(var[i] == enc[i])
while True:
if s.check() == sat: # 找到解
m = s.model()
ascii_list = [m[input[i]].as_long() for i in range(34)] # 将Z3的符号值转换为Python的普通整数
flag = "moectf{" + "".join(chr(ascii_list[i]) for i in range(34)) + "}"
print(flag)
# 添加阻塞条件,寻找下一个解
block = []
for i in range(34):
block.append(input[i] != m[input[i]])
s.add(Or(block)) # 至少有一个变量与当前解不同
else:
break
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
from z3 import *
def solve():
a = [Int('a%d' % i) for i in range(10)]
s = Solver()
s.add(2 * a[7] + 8 * a[6] + 8 * a[5] + 2 * a[4] + 4 * a[3] + 5 * a[1] + 2 * a[0] + 6 * a[2] + a[8] + 5 * a[9] == 3976)
s.add(a[5] + 9 * a[3] + 7 * a[2] + 5 * a[1] + 3 * a[0] + 7 * a[4] + 4 * a[6] + 6 * a[7] + 8 * a[8] + 5 * a[9] == 5265)
s.add(7 * a[8] + 2 * a[6] + 6 * a[4] + 7 * a[3] + 7 * a[2] + 3 * a[1] + 8 * a[0] + 5 * a[5] + 4 * a[7] + 9 * a[9] == 5284)
s.add(7 * a[6] + 5 * a[5] + 6 * a[4] + 3 * a[3] + 9 * a[0] + 6 * a[1] + 4 * a[2] + 9 * a[7] + 8 * a[8] + 7 * a[9] == 5925)
s.add(7 * a[8] + 8 * a[6] + 6 * a[4] + a[2] + 4 * a[1] + 3 * a[0] + 2 * a[3] + 5 * a[5] + 2 * a[7] + 3 * a[9] == 4048)
s.add(3 * a[8] + 9 * a[7] + 7 * a[6] + 4 * a[4] + 4 * a[3] + 5 * a[0] + 8 * a[1] + 6 * a[2] + 4 * a[5] + 7 * a[9] == 5072)
s.add(5 * a[7] + 2 * a[3] + 2 * (a[0] + a[1]) + 3 * a[2] + a[4] + 7 * a[5] + 2 * a[6] + 3 * a[8] + 2 * a[9] == 2813)
s.add(3 * a[8] + 5 * a[7] + 7 * a[6] + 3 * a[5] + 7 * a[4] + 7 * a[1] + a[0] + 7 * a[2] + 8 * a[3] + 6 * a[9] == 5004)
s.add(2 * a[8] + 5 * a[6] + 5 * a[5] + 5 * a[4] + 9 * a[3] + 5 * a[0] + 9 * a[1] + a[2] + 5 * a[7] + a[9] == 4490)
s.add(6 * a[8] + 7 * a[7] + 5 * a[6] + 6 * a[3] + 4 * a[1] + 6 * a[0] + 8 * a[2] + 6 * a[4] + 8 * a[5] + 7 * a[9] == 5936)
for i in range(10):
s.add(a[i] >= 32)
s.add(a[i] <= 126)
if s.check() == sat:
model = s.model()
solution = [model.eval(a[i]).as_long() for i in range(10)]
print(solution)
for item in solution:
print(chr(item),end='')
if __name__ == "__main__":
solve()
|






 Lunatic
Lunatic